How to build a well-designed modular Digital Twin Software based on algebraic composition

December 29, 2023 | 10:22 AM

The aim of this post is to describe a theoretical approach – the Linear Software Models of Composition to build a well-designed modular Digital Twin Software.

Linear Software Models are the simplest theoretical models of software composition. Systems obeying such a model are composed just by addition of independent modules. A central concept in Linear Software Models is linear independence. Linear independence is the formal algebraic equivalent to the informal software engineering concept of uncoupling.

The theoretical standard proposed by Linear Software Models for each software system is a square and block-diagonal Modularity Matrix for the respective system. The Modularity Matrix is a mathematical representation of the software system’s architecture. It is a square matrix with columns and rows corresponding to the system’s structors and functionals, respectively. The Modularity Matrix is a binary matrix, with 1-valued elements indicating the presence of a link between a particular structor and functional, and 0-valued elements indicating the absence of a link.

An important consideration for software system design analysis is to use the Modularity Matrix itself as a source of quantitative criteria to evaluate the modularity of a given design for a software system.

Table of contents

Open Table of contents

Modularity Matrix

In a Linear Software Model, there are two main concepts: one for software structures and another for software functions. The Modularity Matrix, which defines their relationship, can be described like this:

Essentially, the Modularity Matrix is an expanded Boolean matrix. In this matrix, each link or connection between a software function (represented by rows) and a software structure (represented by columns) is marked with a value of 1. Conversely, if there is no link between a particular function and structure, this absence is denoted by a value of 0 in the matrix.

digital-twin-modularity-matrix

In this theoretical framework, a software system’s architecture is defined by two primary entities: structors and functionals.

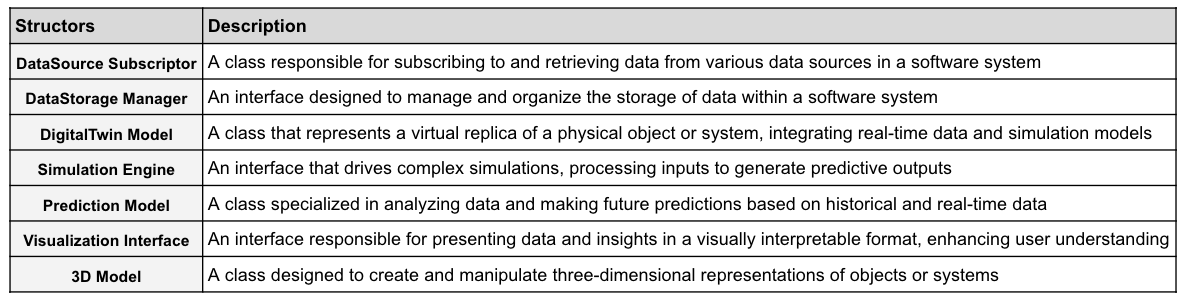
The term ‘structors’, drawing a parallel with the concept of vectors, and represents the architectural units from a structural perspective. They extend the idea of a structural unit to encompass a variety of types such as structs, classes, interfaces, and aspects, as well as hierarchical groupings like sets of classes and design patterns. Structors are more about types rather than specific instances and are components that can be loaded into the software.

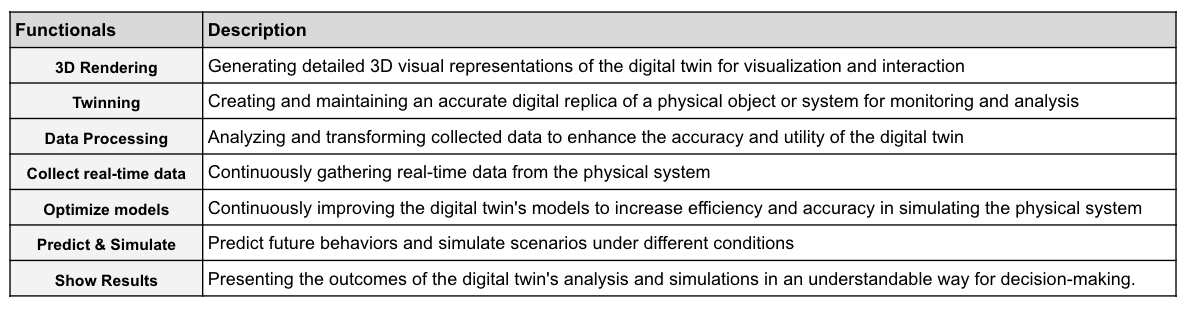
On the other hand, functionals are seen as the architectural units from a behavioral standpoint. They represent potential functions within the system, describing the possible actions or behaviors that could be executed, but it’s not mandatory that they are always invoked or utilized. This distinction highlights the diverse roles and functionalities within a software system’s architecture

When a Modularity Matrix displays separate, non-overlapping sets of dependencies, it is possible to organize structors and their corresponding functionals into distinct modules. In this arrangement, the sets of structors (akin to vectors) in each module are linearly independent from those in other modules. This organizational method simplifies the matrix into a block-diagonal format. In this format, as illustrated in figure, the matrix is composed of smaller square blocks of varying sizes positioned along the diagonal of the matrix. Each block represents a module, and the linear independence between modules is visually evident in this block-diagonal structure.

digital-twin-modularity-matrix

By definition, software structors are elementary software artifacts, which the software engineer decides to look at them as indivisible into smaller structors. A certain structor is not split into specific mathematical processes such as prime factorization or modulo arithmetic, although decomposition is clearly possible. The same principle applies to functionals.

Software quantitative criteria to evaluate the modularity

List of concepts and results obtained within Linear Software Models in order to have basic equations and calculation procedures.

Single Responsibility

In a strictly block-diagonal modularity matrix each structor column intersects a single module. Similarly, each functional row intersects a single module. This theorem is easily verified. It means that a single module is responsible for providing each functional exclusively by its structors. This is the Single Responsibility Principle (SRP) applied to modules.

Cohesion

The cohesion of a Software System Module, at a given abstraction level, is determined by:

Sparsity: an important property of the Modularity Matrix of software systems, which is a consequence of cohesion, is that the matrix is sparse. Module Sparsity = Number of zero-valued elements / Matriz size

i.e. large numbers of zero-valued matrix elements relative to the matrix size. Sparsity of a module or of the whole Modularity Matrix can be quantitative criteria within algorithms and to verify Modularity Matrix trends with size.

Coupling

Means that less 1-valued matrix elements are found in the same row or same column within a module. Operational decoupling – the operational meaning is the removal of linear dependencies, by some suitable action. This action may be addition or removal of architectural units and/or links between units.

Composable Functional

A software functional is considered independently composable, or simply composable, with respect to structors under certain conditions. This occurs when it aligns with a specific, non-empty subset of system structors. This subset is identified by the presence of 1-valued links in the functional’s corresponding row within the Modularity Matrix. Additionally, for a software functional to be independently composable, it must exhibit linear independence from the other rows in the Modularity Matrix. This means that its composition or relationship with structors is unique and not directly dependent on or similar to the compositions of other software functionals in the matrix.

Diagonality

The diagonality of a Modularity Matrix (M) is taken as a quantitative expression of the software system modularity.

diagonality

Offdiag is a sum over 1-valued Mjk off-diagonal elements of the square N*N Modularity Matrix M, multiplied by the absolute value of the difference between each element’s row j and column k indices. The overall matrix offdiag is a double sum over rows and columns:

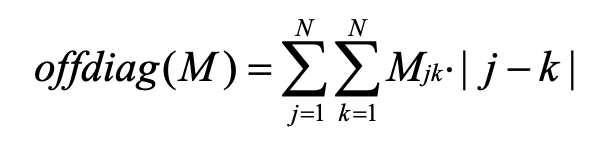
offdiag

Since the standard Modularity Matrix is block-diagonal and its simplest case is strictly diagonal, we measure the modularity by a distance criterion from the strictly diagonal Matrix. The more positive the Diagonality, the more modular a particular design of the software system under analysis.

Digital Twin Case Study

The goal of this section is to demonstrate the power of Linear Software models and Modularity Matrix, showing by a case study of concrete Digital Twin software architecture.

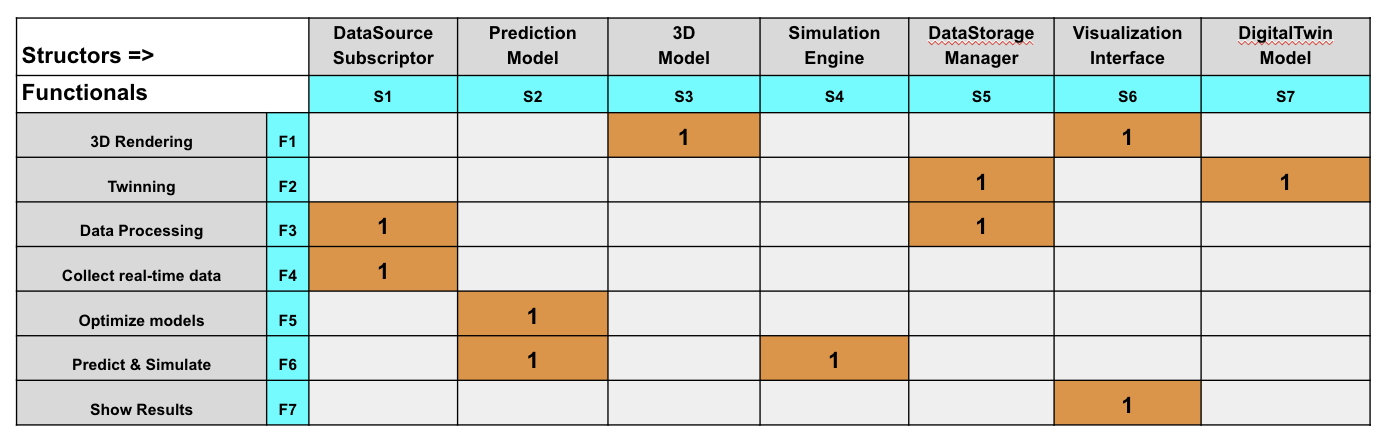
Below is an illustrative example of Digital Twin structors and functionals:

digital-twin-structors digital-twin-functionals

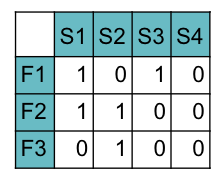
An initial Modularity Matrix:

digital-twin-modularity-matrix

Pure algebraic row/column reorder, without semantic concerns, brings about the almost blockdiagonal Matrix.

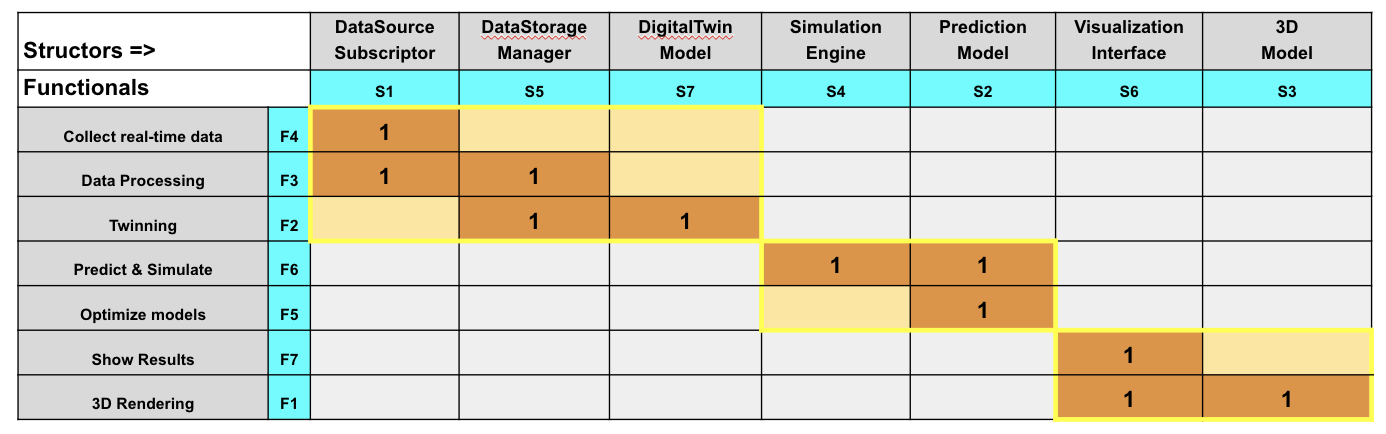
digital-twin-modularity-matrix

This case study shows that a algebraic reordering, without prior semantic knowledge, obtains plausible modules.

Its modules – diagonal blocks – are:

All modules apply the Single Responsibility Principle (SRP). Each structor (column) intersects a single module. Similarly each functional (row) intersects a single module.

Diagonality(M) = 7 - 4 = 3

Composability:

References